Even though the knowledge level, namely that in the technical branches, has almost reached its very top in the last years owing predominantly to the computer analyses and simulations, we can still observe greater or smaller anomalies in the area of an engine-gearbox co-operation in relation to a total drive output even in not only the most prestigious formula-series teams worldwide.

So let’s take a closer look at the physical causalities of transmission of both engine torque and output to the wheels of the vehicle while all of our conclusions will be valid in full generality for any racing machine with multi-speed gearbox starting from F1 car up to a go-kart, Rally Special, autocross buggy or also a motorcycle. On Fig. 1 we can see a traction layout with representations of important variables that we will use in the following text. We may also employ a clever but quite simple method to avoid the necessity to work the dynamic process influences into our contemplations – the method to always describe the instantaneous status so that finding the drive output peak in the given moment will at the same time mean a drive output peak in terms of “the quickest possible attainment of destination point” which is just the thing the designers of Competition Specials are getting at first of all.

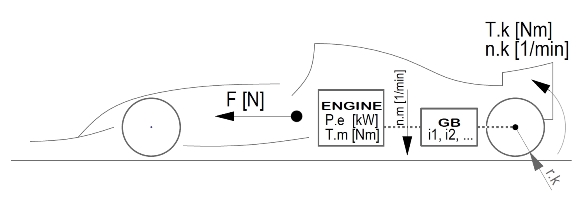
Fig. 1 reveals an engine characterized by specific output Pe[kW] (effective) and specific torque Tm[Nm] at specific speed nm[1/min], then a gearbox (designated as GB) that transmits the engine torque to the wheels to multiply the torque by transference number ic (spread; it equals to the product of a gear ratio of individual speed gear and a permanent differential gear), and finally the driven wheels of a radius rk[m] which the torque Tk=Tm*ic is being realized upon (we remind the matter of course that the output is not influenced by the gear while the torque is influenced by the gear). As a result of adhesion and torque on wheels the driving power F[N] is induced which is the most important variable in the entire traction process:

It is apparent that the force F[N] (acting in the vehicle’s gravity centre) must be the greatest possible in every moment for the vehicle (car, motorcycle, …) to be able of a maximum acceleration (or for a car to be able to negotiate the steepest slope possible at a given velocity). The question we are going to find an answer to now is in what mode the engine must be operated to obtain the maximum driving power for the given velocity of a vehicle.

Because the wheel radius rk is a constant without parameter influence on our conclusions, we can accept the proportion below:

This means that the force acting on the vehicle will be maximum in a specific moment if the product of the engine torque and the spread from engine to wheels is maximum then – with regard to Remark 1 in this text’s introduction – the maximum drive output will be attained in this case as well.

It is of set purpose that we leave the parentheses of variables in relationship (2) speaking of a product as a whole since it is just this circumstance that will lead to quire unexpected conclusions in the following text.

Let’s take a look at the problems from rather different side for this will give us chance to explain very important energy conditions and relations as well. Let’s have a car of a weight of m[kg] on a hill’s base, Fig. 2 leaving the car go to this hill''s top directly (case a)) and along a spiral (case b)).

It is obvious that in case a) the car will go slowly, say at the 1st speed gear thus covering the shortest possible distance. On the contrary, in case b) the car will go fast, say at the 4th speed gear covering in doing so markedly longer distance. In both cases we have to “put” the same energy E=m*g*h[J] in the car to relocate the mass m (car) from point 0 (hill’s base) to a height h (top of the hill). This energy is really the same for both the cases- it is not dependent on either the driving distance or velocity, it depends exclusively on the hill''s height h[m] and the car’s weight m[kg]. But if the cars from case a) and case b) are to race with each other, then we are interested in the time in which the cars get to the hill’s top and new variable is brought to our play – the output as proportion of energy and time:

Logically- the shorter the travelling time should be the greater must be the output the car keeps at disposal, P~(1/t).

Given the fact that, in the Newton’s physics, the following basic formula applies for driving power

and with regard to the fact that we relate our theories to the instantaneous status at a constant velocity w[m/s] (see Remark 1) we can accept proportion F=const*P, thus F~P. And just how we said in the article’s introduction- the only possible result of designers’ efforts is ensure the driving power (consequently “drive output”) is maximum:

Relationship (5) has enormous meaning in the technical practice since it shows that operating an engine in the area of output peak is the only way to either attain the driving power peak on the wheels of vehicle (go-kart, motorcycle, buggy, …) while the engine torque has absolutely no importance!

To support our statement even more, let’s get back to relationship (2) that characterizes the traction conditions yet rather more transparently than the slightly abstract reflection with the cars under the hill. According to (2) it would seem at the first sight that it is just engine torque (not its output) that is the essential and important variable here for the attainment of maximum driving power F[N] on the vehicle’s wheels. However, this statement would be a fatal mistake since what must be considered is the fact that a total transference number ic contained in relationship (2) is, to considerable extent, a selectable variable which influences directly the resultant driving power which is why we clung so vigorously to the importance of parentheses in a product (Tm*ic) when interpreting the relationship (2) in the article’s introduction.

Let us prove the “essentiality” of output and the unsubstantiality of engine torque by using simple mathematics and Fig. 3 upon which is represented a possible fractional characteristics of F1 2008 engine.

You can see several characteristic points in the graph: torque peak point that is characterized by speed nT (~14000/min), torque peak Tmax (~320Nm) and matched output PT (=320*14000*(3.14/30)=470kW). What we have further there is the output peak point characterized by speed nP (=19000/min), by maximum output Pmax (~560kW) and the matched torque TP (=560exp+03/19000*(30/3.14)=280Nm). What we have further plotted in the graph are two conditions designated (A) and (B) where speed 16000 rpm, output 510kW and the matched torque 510exp+03/16000*(30/3.14)=305Nm are segregated for condition (A) and speed 18000 rpm, output 550kW and torque 550exp+03/18000*(30/3.14)=290Nm are segregated for condition (B). We will compare now in which of the engine operating cases we are to reach the maximum driving power F[N] at a constant velocity.

Let’s imagine such initial state where the vehicle moves say to the 5th speed gear at a velocity of 230 km/hr, for example, while the engine is run in condition (A), that is, at a speed of 16000 rpm. Under these conditions the formula i5=iA=nm*(3.14/30)*rk/w will apply for transference number 5°, thus, iA will equal 16000*(3.14/30)*0.31/(230/3.6)=8.13 and, according to equation (1) we have got driving power F[N] in the operation point (A) that is equal to the product below

Let’s imagine now that, having still the same velocity of 230 km/hr, we change down to the 4th speed gear; the engine speed increases to 18000 rpm so we proceed to the operation point as described by condition (B) in the graph according to Fig. 3. Now the transference number i4=iB equals 18000*(3.14/30)*0.31/(230/3.6)=9.15 and the driving power according to (1) for condition (B) will be:

FB = (TB * iB) / rk = 290*9.15/0.31 = 8560 N,

so that operating the engine in condition (B) lead in fully unambiguous manner to the attainment of greater driving power on the vehicle’s wheels and thence the consequent vehicle’s acceleration will be higher that by operating the engine in condition (A). It holds true even though the engine, while in condition (B), generates lower (!) torque (290 Nm) in comparison to condition (A) (305 Nm).

Let’s count, for the sake of interest, also the driving power for the operation points of both torque peak and output peak, again for the same velocity of 230 km/hr:

speed nT=14000rpm: gear ratio=14000*(3.14/30)*0.31/(230/3.6)=7.11, driving power=320*7.11/0.31=7340N,

speed nP=19000rpm: gear ratio=19000*(3.14/30)*0.31/(230/3.6)=9.65, driving power=280*9.65/0.31=8715N.

If we compare our results we can see that we gradually get resultant driving powers 7340N, 8000N, 8560N, and 8715N for operating conditions of Tmax, (A), (B), and Pmax characterized by speed nT, nA, nB, nP, and that the amounts of driving powers copy the performance curve (in accurate conformity with the conclusion according to (5)) and not the torque curve as many times misinterpreted fatally even in the expert circles. And- what is it that actually happened? It was just and only thing – by increasing the service speed (presuming the output is rising) the torque drop is lower than transference number increase (at a specific velocity) and thence the product (Tm*ic) is higher in that engine’s operation point where the output is higher, even though the engine torque’s value Tm is lower here. Among others we have also proved how silly would be the effort to fall into the torque peak speed nT during gear change to higher speed gear (see Fig. 3), let alone operate the engine in the area of peak torque because this would for sure make us finish last in this case…

The reason why equation (1) cannot be used for immediate drawing a definite conclusion on whether or not the torque is suitable consists in the fact that two variables are contained here and they condition each other (from mathematical point of view it is one equation in two unknowns); if we are to use this equation for drawing definite consequences then we would have to transpose the equation using the relationship between output and torque P=T*ω=(π/30)*T*n into the shape below

since we’ve got already only a definite single variable here, namely the output. This is because the ratio (ic/nm) is a constant number for a constant velocity (compare: for the operation point Tmax according to Fig. 3 it is ic/nm=7.11/14000=508exp-06, for condition (A) it is ic/mn=8.13/16000=508exp-06, for condition (B) it is ic/nm=9.15/18000=508exp-06, etc.). Naturally, the equation (6) in this case confirms the conclusions expressed in the process of deriving the relationship (5) since (ic/nm)=const, (30/π)=const, rk=const, and equation (6) lapses automatically in to the shape (5) that was previously derived using different method.

However, equation (6) has one more relatively important significance if only it is a little bit modified into the shape below

F * rk = Tk = (30/π) * Pe * (ic / nm) [Nm; W, 1/min] (7),

because we are capable of establishing immediately the torque Tk[Nm] on wheels from performance curve and transference number only without knowing the engine torque behaviour! That is to say, the conclusions we uttered for driving power F are in fully unambiguous manner transferable to the torque on wheels Tk[Nm] as well and we can speak aloud several basic axioms the none correctly designed engine-transmission co-operation as a whole can get along without fulfilling them:

(1) It is essential for a maximum drive output of a vehicle (car, motorcycle, buggy, ...) to reach the maximum driving power F[N].

(2) It is essential for a maximum drive output to reach the maximum torque Tk=(Tm*ic) on the car wheels.

(3) The amount of engine torque IS NOT ESSENTIAL for a maximum drive output.

(4) The amount of product of engine torque and specific transference number is essential for a maximum drive output, i.e. (Tm*ic).

Furthermore, let’s compare for the sake of interest the resultant torque on the driven wheels at a velocity of 230 km/hr in the operation points according to Fig. 3:

Speed nT: Tk=(30/3.14)*470exp+03*(7.11/14000)=320*7.11=2275Nm,

Speed nA: Tk=(30/3.14)* 510exp+03 *(8.13/16000)=305*8.13=2475Nm,

Speed nB: Tk=(30/3.14)*545exp+03*(9.15/18000)=290*9.15=2645Nm,

Speed nP: Tk=(30/3.14)*560exp+03*(9.65/19000)=280*9.65=2715Nm.

Please take note of the fact that by operating the engine in the torque peak point (speed nT) we get to the clearly worst result in terms of the attainment of drive output peak (in accordance with Remark 1) and, as compared to the operation in the output peak point (speed nP) we lose a whole 16 % in the traction!

To deliver yet at least one positive feature with regards to engine torque, let’s however, give at least one reason why the torque must be dealt with by designers at specific designing stages. What is in question is dimensioning and strength analyses of the parts which participate in the traction since this branch cannot get along without a knowledge of the amount of incoming torque so far. However, the engine torque as a value on itself cannot be used for anything else.

We hope to have been at least partially successful in tearing down one of the silliest motorsport-related myths that is most dangerous for the racers longing for victory, that is, the myth of “need for sizable twist”, and let’s hope that the traction designers for any type of motorsport branch (that is, with exception of speedway and machines with transmissionless drive system) will at least respect the conclusions uttered herein.